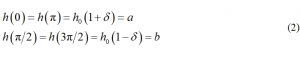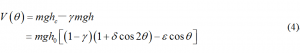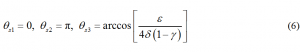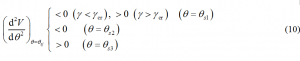？

水中竖蛋与拉格朗日定理

？

刘延柱1)

（上海交通大学工程力学系？ 上海？ 200240）

鸡蛋的形状接近一个长椭球，只能平卧在桌面上，很难竖立起来。虽然竖蛋并非绝无可能，但成功的案例多因各种辅助因素起了作用^[1]。从能量角度分析，直立的鸡蛋稍有倾斜，重心即下降，可见直立状态的重力势能为极大值。平卧的鸡蛋如朝两头倾斜则重心上升，表明平卧状态的势能为极小值。如沿圆周方向偏移，因重心高度不变，势能也不变而处于随遇平衡状态。
应用拉格朗日的稳定性定理，不难从理论上对上述现象作出解释。拉格朗日定理指出：如保守系统的势能在平衡位置处取孤立极小值，则平衡位置是稳定的^[2]。满足一些补充条件时，其逆定理也能成立^[3]。
将鸡蛋放进水里，情况就有些复杂，因为出现了与重力方向相反的浮力。鸡蛋的比重大于水的比重，放进水里就要沉底。鸡蛋一头稍尖，一头稍钝，钝头处有个小气室。所以鸡蛋的重心朝尖头方向稍稍偏离椭球的几何中心。不同作用点的浮力与重力构成力偶，将鸡蛋的钝头稍稍抬起，而不是平躺在水底。如果改变浸泡鸡蛋的液体成分，随着液体比重的升高浮力增大抬起的角度也随之增大。不断增大液体的比重，使钝头不断往上抬，如能抬高到垂直位置，竖蛋问题也就能在水中得到解决了。
要分析鸡蛋在水中的平衡状态和稳定性，拉格朗日定理仍可以应用。因为讨论静力学问题可忽略流体动力效应。仅考虑保守性质的液体浮力时，水中的鸡蛋仍属于保守系统。
讨论这个问题的关键是要对鸡蛋的几何形状作出适当的数学描述。因为鸡蛋倾斜时接触点沿蛋壳移动的规律完全取决于蛋壳的外形。将蛋壳视为长短半轴为和的旋转椭球曲面。先将鸡蛋的尖端竖在台面上（用手扶住不让它倒下），慢慢转动，直到它的侧面与台面接触，鸡蛋的几何中心距台面的高度必不断减小。如继续朝原方向转动，点的高度又开始增大直至钝头与台面接触。将鸡蛋的尖端至钝端的对称轴记为轴，其相对垂直轴的角度记为，则点高度随角先减小后增大的变化规律可用函数近似地表示为

对于尖端或钝端触底和侧面触底两种情况，分别有

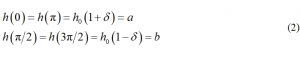
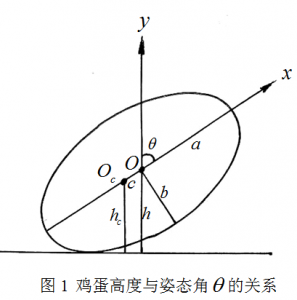
从中导出，。公式(1)所描述的鸡蛋并非严格按数学定义的椭球，但已足够接近鸡蛋的实际形状且便于数学处理（图1）。
设鸡蛋的重心偏离几何中心的微小距离为，令，则点的高度为

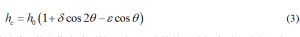
忽略小气室的影响，将重量除以体积作为鸡蛋的比重。设液体的比重与鸡蛋比重之比为，如鸡蛋的重量为，则液体的浮力为。离水的鸡蛋是的特例。限制为小于的参数，因为如，鸡蛋将在液体中悬浮，甚至部分浮出液面与沉底的前提发生矛盾。由于重力作用于质心，而浮力作用于几何中心，鸡蛋的总势能为

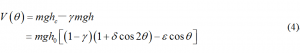
根据拉格朗日定理，先计算的极值条件

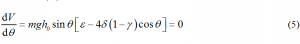
此条件的3个解对应于3个可能平衡位置

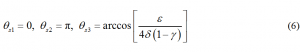
其中的平凡解和表示尖端触底和钝端触底的两种直立状态。非平凡解表示侧面触底状态，其存在条件为

此条件要求参数小于某个临界值
，　　　　　　　　　　　　　 　　
就水的情况而言，因远小于，条件(7)必能自动满足，接近且稍小于。如增大液体的比重，则随的增大，即随液体比重的增大而减小，钝端趋于向上抬起。在的临界情形，而与竖直状态的完全重合。如，因不满足条件(7)，非平凡解即不复存在。
为判断平衡状态的稳定性，必须计算的2阶导数，得到

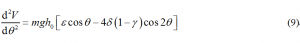
将式(6)表示的各平衡状态代入上式，得出

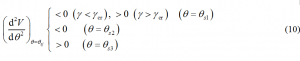
应用拉格朗日定理判断，重心在浮心上方的直立状态的势能为极大值，为不稳定平衡，侧卧的的势能为极小值，为稳定平衡。浮心在重心上方的直立状态的稳定性则取决于液体的比重。液体比重小于临界值时，即使浮心在重心上方也不能稳定，当比重增大到时此直立状态方能稳定。
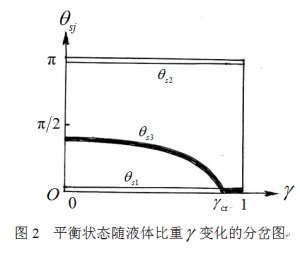
图2为鸡蛋的平衡状态的位置及其稳定性随参数变化的静态分岔图，以实心线和空心线表示稳定和不稳定平衡。临界值成为参数影响平衡状态的分岔点。时原来的3个平衡位置减为两个，且原来不稳定的转为稳定。可见浮力的出现有助于鸡蛋的稳定，但液体比重必须超过临界值，方能使低重心的竖直状态成为稳定平衡。水中竖鸡蛋也仅在此特殊条件下方有可能实现。此稳定性条件也包括，即液体与鸡蛋比重完全相同的特殊情形。此时鸡蛋可解除底面约束，以浮心高于重心的竖直状态悬浮在液体中。

？

参考文献
[1]？？？？？？ 刘延柱. 立春时节话竖蛋. 力学与实践，2013，35(1): 97-98
[2]？？？？？？ 刘延柱. 高等动力学. 北京：高等教育出版社，2001
[3]？？？？？？ 王照林. 运动稳定性及其应用. 北京：高等教育出版社，1992



图1 鸡蛋高度与姿态角的关系？？？？？？？ 图2　平衡状态随液体比重变化的分岔图

---