应用数学和力学的结合-
弹性力学建模和解法
嵇 醒
(同济大学 航空航天与力学学院, 上海200092)
1引言
钱伟长
[1-3]始终把提升和发展中国力学放在心上。年过七旬,他创办了《应用数学和力学学报》之后,又创立了应用数学和力学研究所。值得注意的是他把学报和研究所都定名为《应用数学和力学》。
钱伟长曾讲过为什么要起名为应用数学和力学研究所?他说:“就是要推动数学与力学继续结缘,以先进的数学工具来研究力学,以力学的进展来推动现代数学的发展”。这是钱伟长一生的力学实践所换来的箴言。
钱伟长讲的《应用数学和力学》是指通过应用数学和力学的巧妙结合以达到应用力学的创新发展。应用数学和力学的结合是钱伟长创新研究的精微所在,这是钱伟长应用力学创新思想的核心。
向钱伟长学习,就是要学习钱伟长的《应用数学和力学相结合》的研究理念。要学习钱伟长的《应用数学和力学相结合》的研究理念,必须首先懂得钱伟长的《应用数学和力学相结合》提法的深刻内涵。
本文以弹性力学的建模和主要解法来探索《应用数学和力学相结合》的深刻内涵,领略钱伟长学术创新的源头,从而提升力学研究的创新能力。
2弹性力学数学模型的建立
弹性力学的基本方程是由法国的物理学家及工程师纳维埃和数学家哥西,泊桑,建立于19世纪20年代
[4,5]。值得一提的是这套基本方程的建立也是数学与力学的巧妙结合。他们把微积分应用于弹性体的变形分析,引入了应变、应力的概念,将弹性体当作连续介质处理,把一个原来是复杂的弹性体受力变形的力学问题巧妙地转化为一组数学的偏微分方程。由几何的位移方程,力学的平衡方程,和弹性体的本构方程归并而成的弹性力学基本方程, 加上三个边界条件, 不多不少,正好可以用来求解15个应力、应变和位移未知函数。创始人的奇迹般的神奇构想,创造了世界上第一个固体力学用偏微分方程表达的数学模型,达到了叹为观止的巧妙程度,从而开创了应用数学和现代力学相结合的时代,开启了固体力学服务于工程的时代。
国家自然科学基金项目(10672122)资助.
Email:
jixing@tongji.edu.cn
连续介质假设是采用微积分建立弹性力学数学模型所必需的。抽象的连续介质假设无视各类材料的材质和微观结构的差异,能够用来解决重大工程结构的强度问
题吗?对此,力学家和工程师采取了二道实验保障:即材料的本构方程必须采用直接来自实验测得的弹性常数,强度理论中用到的材料强度参数也必须采用直接来自材料试验测得的性能参数。数学求解弹性力学方程时采用虚构的连续介质假设,但
在把这种结果应用于工程时,已经回归到真实材料试验测得的性能数据,这就是弹力学和固体力学在工程应用中取得成功的秘奥。于是,数学、力学、和工程达到了完美的结合。
由于弹性力学中采用了连续介质假设,强度校核中用到的材料失效判据不可能是基于物理的失效机理,而只能是采用以力学实验为基础的力学判据。由此可见,固体力学对于力学实验的依赖性。
任何复杂的工程结构的强度分析都可归结为固体力学问题:先按弹性力学的数学模型对数学方程求取解答,再按真实结构材料的实测强度性能进行强度校核,这是何等省力、精巧、聪明的事情。否则,单凭经验,现代工程结构设计将会处于何等艰难的境地。
弹性力学数学模型的建立,从此使应用数学和力学结成了不解之缘。
3 19世纪弹性力学的发展-半逆解法
弹性力学基本方程建立之后,对弹性力学边值问题的数学解析求解成为数学家和力学家面前的一道难题。穷尽所有偏微分方程的解法理论,找不出一套可以用来求解弹性力学基本方程的普适方法。无奈之下,弹性力学只能对具体的问题,由易到难,逐个进行研究,寻求给定边界条件下的特解。最初的一批结果得自逆解法(试凑法),逆解法不经过数学求解过程,直接猜出能满足全部弹性力学方程和边界方程的解答。例如:简单拉伸和纯弯曲
[4]。逆解法的根据是克希霍夫唯一性定理,而克希霍夫唯一性定理的证明是以弹性势的存在和叠加原理为基础的
[4],换言之,这是力学家用力学的理由来绕过唯一性定理的数学证明的困难。对于稍微复杂一点的问题,逆解法很难奏效,所以弹性力学遇到了难以克服的数学困难而发展缓慢,难以满足工程应用的需求。
圣维南非圆截面轴扭转问题的半反演法
[4]对弹性力学起到了绝处逢生的作用。从此在随后的数十年里,半反演法成为弹性力学求解的必经之途,开启了弹性力学各类问题的解答的丰收期。
圆截面轴扭转问题在材料力学中,用平面截面假设就可以解决。平面截面假设说的是圆轴受扭转时截面作整体相对旋转且保持为平面。根据材料力学平面截面假设,圆轴扭转的位移表达式是
u =-
qzy ,
v =
qzx ,
w =0? , (1)
q是单位扭转角。由此位移表达式求出截面上剪应力的方向与半径垂直,大小与到圆心的距离成正比,其它应力分量均为零。用圆轴扭转的位移表达式(1)代入弹性力学基本方程和圆轴扭转的边界条件,能够全部满足,所以它碰巧是弹性力学的精确解。平面截面假设其实就是弹性力学的逆解法,把应力的分布规律全都猜到了。
用这个位移表达式来处理非圆截面轴的扭转问题,却不能全部满足弹性力学方程和边界条件,所以,它不是非圆截面轴的扭转问题的解答。以矩形截面轴扭转为例,在截面周边的剪应力必须和截面周边平行,在矩形截面的四个角点处剪应力必须为零,这是矩形截面轴侧面为自由的边界条件所要求的,但是用平面截面假设的结果与此不符。
非圆截面轴的扭转问题是三维的弹性力学问题,需要满足三维弹性力学基本方程,和非圆截面轴扭转问题的边界条件。但是没有人能对此数学问题进行解析求解,求解方法不存在。也没有人能猜出非圆截面轴的扭转的应力分布规律,试凑法对此也无能为力。非圆截面轴的扭转问题成为当时久攻不下的难题。
圣维南却另辟蹊径,既不全部套用圆轴扭转的试凑法和平面截面假设,也不放弃其适用的部分。对圆轴扭转的位移表达式(1)进行了恰到好处的改造。他对非圆截面轴扭转的位移表达式改为
u =-
qzy ,
v =
qzx ,
w =
q j(
x,y) , (2)
j(
x,y)是未知的截面翘曲函数,
q是未知的单位扭转角。求解非圆截面轴扭转问题,就是要确定未知的
j(
x,y)和
q。
位移表达式(1)和(2)的差别,只在于圆轴扭转时原来是平面的截面保持为平面,而非圆轴扭转时原来是平面的截面发生了翘曲。由于非圆轴扭转时原来是平面的截面发生了
j(
x,y)的翘曲,使得截面上的剪应力分布与平面截面假设不一样,而其余的应力分量未受影响,依然是零。圣维南放松了平面截面假设,
j(
x,y)翘曲函数的作用是用来调整截面上的剪应力分布,使得非圆截面轴侧面自由的边界条件得以满足。位移表达式(1)和(2)的这点差别导致解法上的巨大变化。位移表达式(1)属于试凑法,而位移表达式(2)中
u和
v用已知函数表示,
w用未知函数
j(
x,y)表示,未知函数
j(
x,y)需要用弹性力学方程来确定,所以称为半反演法。。
由式 (2)所推导的扭转应力自动满足协调方程,而弹性力学平衡方程则简化为一个翘曲函数
j 的拉普拉斯方程:

根据轴的侧面自由的边界条件,可导出关于翘曲函数
j 的边界条件:
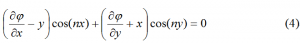
式中,
n是截面边界的外法线方向。
由方程(3)和边界条件(4)求得翘曲函数
j 后,剩下的未知单位扭转角
q由杆端的扭矩
Mz决定。
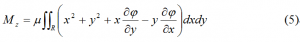
到这里,一个复杂的三维弹性力学扭转问题已简化为只需要求解一个翘曲函数
j 的二维拉普拉斯方程(3)和边界条件(4)所表示的诺伊曼(Neumann)问题,扭转方程(3)和边界条件(4)就是由全部三维弹性力学方程及边界条件,经过圣维南半反演法得到的简化方程,二者是等价的。由半反演法得到的解析解,能够满足全部三维弹性力学基本方程和边界条件,所以是严格精确的,没有引入误差。很多具体的非圆截面柱体扭转问题都是用这个简化方程求解得到的。
值得注意的是:由位移表达式(2)出发,推导方程(3-5)是轻而易举的。由(3-5)式所表示的非圆截面柱体扭转方程是对弹性力学基本方程的简化,并且简化到惊人的程度,到了无法再简化的程度,而这套简化方程又是精确的,和全部三维弹性力学基本方程等价。还值得注意的是:这个简化过程是从力学概念出发而得,如果没有位移表达式(2),任何纯数学的推演,都无法从三维弹性力学基本方程推导到扭转问题的简化方程(3-5)。
这个圣维南简化的奥妙全在于位移表达式(2)。有了位移表达式(2),简化方程的推导变得可能而省力,没有位移表达式(2),弹性力学方程的简化就无法进行。所以位移表达式(2)是非圆截面柱体扭转问题半反演法的关键。也是圣维南研究非圆截面柱体扭转问题的理论创新的核心。
综上所述,半反演法的实质是:对有些力学问题的某些应力或位移分量作出预先的判断,据此简化弹性力学基本方程,建立一个简化的数学模型,所得简化方程与三维弹性力学基本方程等价,然后用数学中的适当方法求解,就能获得严格的弹性力学精确解。
从此半反演法成为弹性力学求解的主要途径,开启了弹性力学各类问题的解答的丰收期。1933年出版的浩瀚巨著:数学弹性理论教程(Love著),书中各类问题的解答都是半反演法的研究结果
[5]。
4 20世纪弹性力学的发展-复变函数解法
弹性力学中的另一类重要问题是平面应变问题和平面应力问题
[4]。对于此类问题位移u,v和应力分量s
x,s
y,t
xy只和x,y有关。引入艾里应力函数U(x, y),
令
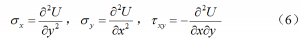
则三维弹性力学方程可以用一个艾里应力函数U的二维重调和方程等价。
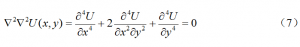
弹性平面问题简化为按边界上给定的面力或位移作为边界条件,求重调和方程(7)的特解。这比起难以下手的三维弹性力学方程来,已经得到了极大得简化。尽管如此,早期的平面问题的解答,诸如简支梁,悬臂梁,旋转圆盘,厚壁圆筒等,是采用直角坐标多项式或极坐标中的一般解,通过逆解法求得的
[5]。直到上世纪30年代,才有了弹性平面问题的正解法——穆斯海利什维利复变函数解法
[4,6]。
弹性平面问题的复变函数解法是应用数学和力学巧妙结合的最为成功的典例。在数学里,复变函数论研究的是解析函数的性质,它不是研究偏微分方程的解法的
[7]。可是,复变函数论里的重要结果却被应用来构造成一种完美的弹性力学平面问题的解法。复变函数论和弹性力学平面问题的这一关系不是一望便知的,复变函数论用来求解弹性平面问题也不是一拍即合的。弹性平面问题的复变函数解法包含了应用数学和力学巧妙结合的精微和曲折,体现了应用数学和力学巧妙结合的艰难。
满足方程(7)的函数叫重调和函数,艾里应力函数U(x, y)是二元重调和函数。复变函数论中,解析函数的充分必要条件是它的实部和虚部满足哥西-黎曼条件,或者说,实部和虚部都是二元调和函数。调和函数满足拉普拉斯方程,一定也满足重调和方程。把复变函数论应用于弹性平面问题的研究就是从这里开始的。
最早的研究成果是:1898年, E. Goursat导出了由二个解析函数j(z)和c(z)表示的任意的艾里应力函数U(x, y),
z=x+
iy ,(8)
1909, G.V. Kolossoff导出了由这二个解析函数j(z)和c(z)表示的应力分量和位移分量的表达式。
下一个走向解法的重要步骤是将平面问题的边界条件也用这二个解析函数j(z)和c(z)表示,以第一类边值问题为例,它的边界条件是:
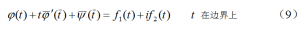
到此为止,在弹性平面问题中,只用到了复变函数论中的哥西-黎曼条件,却已经完成了将物理平面里求实函数U(x, y)的问题,等价变换到复平面里求解析函数j(z)和y(z)的问题。人们不禁要问:这样的变换有意义吗?弹性平面问题对力学家来说,是一个概念明明白白的问题,现在却变成了一个物理概念难以捉摸的复变函数问题,而且,现在只能从一个边界条件(9)来求出二个未知解析函数j(z)和c(z),因为此外已经没有其它有关未知函数j(z)和c(z)的关系了。如果不能从一个边界条件(9)求到二个未知的解析函数j(z)和c(z),那么,以上的这套推导就是无用之功。
现在,成为解法的关键一步是怎样从一个边界条件(9)求到二个未知的解析函数j(z)和c(z),即怎样用边界条件(9)可以唯一确定二个未知的解析函数j(z)和y(z)。熟知复变函数论的人,都清楚解析函数具有实函数无可比拟的优异性质,正是由于解析函数的特殊性质,导致了用边界条件(9)唯一确定二个未知的解析函数j(z)和y(z)成为可能。
复变函数论中有一个哥西积分公式:

式中,C是域R的周边,
a是域R的一个内点,是定义在域R上的解析函数,哥西积分公式说明解析函数在域内任何一点的值可以由其边界上的值通过哥西积分公式获得。这是只有解析函数才具有的性质,这个性质对于用边界条件(9)来确定二个未知的解析函数j(z)和y(z),是极为重要的。
根据哥西积分公式可以直接推出这样的事实,即解析函数j(z)和y(z)可以展开为泰勒级数。
对于一个弹性力学平面问题的圆域问题,边界条件右端项可以在圆周上展开成复三角级数,
s 在圆周上

再把解析函数j(z)和y(z)在圆域展开为Taylor级数:

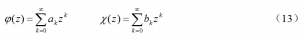
把泰勒级数(13)中的z换成s,和复三角级数(12)一道代入边界条件(9),比较同类项的系数,可以全部确定泰勒级数(13)中的未知系数
ak 和
bk 。
这里,穆斯海利什维利巧妙地利用了复变函数论中的哥西-黎曼条件,哥西积分公式和解析函数的泰勒级数,完成了弹性平面问题的圆域问题的正向解析求解。在此之前,复变函数论的数学里没有用哥西-黎曼条件,哥西积分公式和泰勒级数求解重调和方程的先例,但是在弹性平面问题中,却把这些数学工具变成了弹性力学平面问题的复变函数级数解法。如果一个重调和方程的边界条件不是(9)式的形式,那么,这套解法可能失灵。这套解法只对边界条件如式(9)那样的重调和方程才适用。由此可见,应用数学和力学的结合是需要费尽心力的。
由于边界条件(9)的右端项只能在圆周上展开成复三角级数,复变函数级数解法只能解决圆域问题,其求解范围受到了极大的限制。幸好复变函数论中,还有一个利器,叫保角变换。单值解析函数

定义物理平面z和像平面z之间的点的一一对应的变换关系。由于这种变换具有保角性,所以叫保角变换。物理平面z的非圆域,可以通过适当的变换函数w(z)变换到像平面z的单位圆。然后在像平面z,用复变函数级数解法求解,得到像平面z的解析函数j
1(z)和y
1(z),再用变换函数w(z)通过逆保角变换,把j
1(z)和y
1(z)返回到物理平面z,得到解析函数j(z)和y(z)。这样,








