蛇年话蛇行
刘延柱1)
(上海交通大学工程力学系? 上海? 200240)
今年是蛇年,有关蛇的话题更添谈论兴趣。蛇无足而能行且行进很快。这种独特的行进方式和蛇的生理构造有关。蛇没有胸骨,躯体可以自由弯曲。蛇全身披着一层角质鳞片,肋骨向前移动可使腹部的鳞片翘起摩擦地面产生推进力。关于蛇行的原理早在上世纪
30年代就已有研究论文发表
[1]。近年来由于蛇形机器人技术的兴起,对蛇行运动的仿真研究和理论分析的文献就更为丰富
[2,3]。
蛇最典型的行进方式是蜿蜒运动(图
1)。当蛇头左右摆动,带动身体向两侧弯曲,形成一个类似正弦曲线的波形向后方传播时,蛇身就能快速向前移动。根据
动力学基本规律,蛇必须在外力推动下才能前行,这外力只能来自
鳞片与地面的摩擦力。问题是侧向滑动引起的侧向摩擦力如何能产生向前的推动力,似有必要作些探讨。

图1 蛇的蜿蜒运动
蛇的蜿蜒
运动过程也就是弹性波沿蛇身的传播过程。在蛇形机器人的研究中,描述蛇身弯曲形状的数学模型称为蛇形曲线(
Serpenoid curve)。以蛇的头部
O为原点,沿蛇身建立向尾部延伸的弧坐标
s,理想化的蛇形曲线是一条以
s为自变量的正弦曲线
[3]
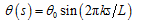 (1)
(1)
其中
为蛇身相对行进方向的倾斜角,
L为蛇身长度,
k为谐波数。
为分析蛇的行进过程,建立随O点平动的
参考坐标系(O-xy)。x轴
沿行进路线指向后方,与弹性波传播方向一致,
y轴为指向右侧的水平轴。蛇在
(x,y)坐标系中的形状可用式
(1)的积分表示
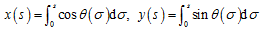 ? (2)
? (2)
为使数学表达更简明,也为表达蛇形曲线随时间的变化过程,将
蛇的蜿蜒
运动设想为沿x轴方向传播的行波,表示为
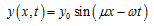 (3)
(3)
其中
=2
/ ,
为沿轴传播的波长, =2
/T,T为传递一个谐波的完成时间,也就是蛇身上同一点往复振动的周期。公式
(2)和
(3)都是对蛇形的近似描述,两种曲线形状相似而不完全相同,但公式
(3)的数学处理要方便多了。
蛇利用侧向滑动获得向前推进力的过程与冰上运动有些相似。当运动员控制冰刀向两侧偏后方滑动时,冰面沿垂直刀刃方向的摩擦力会出现向前的分量推动运动员前进。因此要解释蛇的前进动力就必须考察蛇的侧向滑动有没有类似的现象。
令式
(3)中保持不变对求偏导,得出蛇身上各点的侧向滑动速度
(x,t)
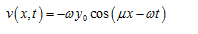 (4)
(4)
为显示
滑动速度 沿蛇身的变化状况,在轴的半波长
/2范围内,根据式
(3),(4)画出某个确定时刻,例如
t=0时刻的蛇形曲线
y(x)和速度曲线
v(x)(图
2)。按正弦规律和余弦规律变化的这两条曲线之间存在 /2相位差。在曲线的两端位移为零,而蛇身相对轴的倾斜角和速度均达最大值。曲线中点的位移为最大值,而蛇身倾斜角和速度均为零。滑动速度过中点后改变方向,在
x的前半段区间(0, /4)内,
v(x)与
y(x)异号,滑动速度与弯曲方向相逆;在后半段区间( /4, /2)内,
v(x)与
y(x)同号,滑动速度与弯曲方向一致。其结果是在的两个区间内,与蛇身垂直的滑动速度分量都偏向蛇尾,与滑动方向相逆的摩擦力都指向蛇头(图
3)。蛇身向左和向右交替向两侧滑动,如同冰上运动员左右脚交替蹬冰的动作,摩擦力就能持续提供向前的动力。
坐标系(o-xy)随蛇平动的牵连速度产生向后的摩擦阻力,当向前与向后的摩擦力互相平衡时,蛇就处于匀速的稳态运动状态。于是蛇的侧向蜿蜒运动能产生前进动力的问题就从物理概念上得到解释。
由此可见,蛇无足而能行的特殊能力与位移和速度之间 /2的相位差有着密切联系。需要补充的题外话是,在人类的科技实践中,不乏利用运动参数的相位差达到设计目的的例子。例如利用液体连通器内液体的振荡与容器摆动之间接近的相位差,以消除陀螺罗经摇摆误差的发明就是著名的成功案例。
图2 蛇形曲线和速度曲线 图3 摩擦力沿蛇身的分布
参考文献
- 1. Mosauer W. On the locomotion of snakes. Science, 1932, 76(1982): 583-585
- 2. Ma S, Araya H, Li L. Development of a creeping snake-robot. Int. J. Robotics & Automation, 2002,17(4): 146-153
- 3. Hirose S, Yamada H. Snake-like robots. IEEE Robotics & Automation, 2009, March: 88-98
Talk on Creeping Locomotion of Snake in Snake-year
LIU Yanzhu
(ShanghaiJiaoTongUniversity, Shanghai 200240, China)







