|
1859年,黎曼发表了《在给定大小之下的素数个数》的论文。这是一篇不到十页的内容极其深到的论文,他将素数的分布的问题归结为函数的问题,现在称为黎曼函数。黎曼证明了函数的一些重要性质,并简要地断言了其它的性质而未予证明。
在黎曼死后的一百多年中,世界上许多最优秀的数学家尽了最大的努力想证明他的这些断言,并在作出这些努力的过程中为分析创立了新的内容丰富的新分支。如今,除了他的一个断言外,其余都按黎曼所期望的那样得到了解决。
现在来说黎曼猜想,在1858年黎曼写的一篇长度只有8页的关于素数分布的论文,在这篇论文中,他提出了有名的黎曼猜想。这猜想提出已有一百多年了,许多有名的数学家曾尝试去证明,就像喜欢爬山的人希望能爬上珠穆朗玛峰一样——因为它的顶峰非常困难到达,目前已有人登上这世界高峰,可是却没有人能证明这猜想!
要想说明黎曼猜想,首先要讲讲这个问题的来源。几千年前人类就已知道2,3,5,7,31,59,97这些正整数。除了1及本身之外就没有其他因子,他们称这些数为素数(或质数),希腊数学家欧几里得证明了在正整数集合里有无穷多的素数,他是用反证法证明,可以参看《数学和数学家的故事》第一集里这个证明。著名的瑞士数学家欧拉,在1737年给了欧几里得定理的另外一个巧妙的证明。
人们早知道下面的调和级数是不收敛(即和是无穷大)。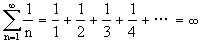
在1737年左右欧拉引进了齐打函数(Zeta function)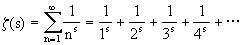
如果令P表示所有的素数集合,即欧拉发现对于S≥1,我们有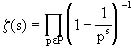 上式的右边表示 上式的右边表示
让p跑遍所有的素数集合,取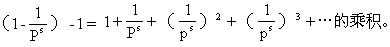 我们看到 我们看到
右边如果展开,每一项是形如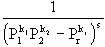 的形状,这里p1,p2,…,pr都是素数。由算术
的形状,这里p1,p2,…,pr都是素数。由算术
的基本原理,我们知道,任何正整数是能表示成素数方的乘积,而这表示法是只有一种。如果素数的个数是有限,则当s逐渐趋近于1时,我们见到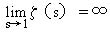 而右边的结果却是有限,这样就
而右边的结果却是有限,这样就
产生了矛盾。由此可知素数的个数不可能是有限的。
在1858年黎曼在他写的唯一一篇关于数论的文章里把齐打函数的定义域扩大到复数域上,他要研究什么样的复数s,能使ζ(s)=0,他在文章里给出了下面猜想,现称为“黎曼猜想”
“所有的非实数的复数s使得ζ(s)=0,,必定在直线Re(s)=1/2 上。”
这个未解决的问题是希尔伯特23个问题中的第8个问题,至今仍没有人证明。对于某些其它的域
,布尔巴基学派的成员已证明相应的黎曼猜想。数论中很多问题的解决有赖于这个猜想的解决。黎曼的这一工作既是对解析数论理论的贡献,也极大地丰富了复变函数论的内容。 德国数学家F.克莱因这样的评价他:“黎曼具有很强的直观,由这天份他超越了当代的数学家,在他的兴趣被激发的领域,他不管是否当局会接受对这研究的肯定,也不让传统来误导他。……他像流星一样出现然后消失,他活跃的时间只不过15年,1851年他完成论文,1862年他生病,1866年他去世。……黎曼的思想,对现代函数论发展的影响是缓慢和逐渐的,他的工作不会在当代引起突然的革命。这主要是由于黎曼的工作是不容易明白,另外是他提出的想法是非常新且奇特的。……”
黎曼的工作直接影响了19世纪后半期的数学发展,许多杰出的数学家重新论证黎曼断言过的定理,在黎曼思想的影响下数学许多分支取得了辉煌成就。
近年对黎曼假设的研究
荷兰三位数学家J.van de Lune,H.J.Riele te及D.T.Winter利用电子计算机来检验黎曼的假设,他们对最初的二亿个齐打函数的零点检验,证明黎曼的假设是对的,他们在1981年宣布他们的结果,目前他们还继续用电子计算机检验底下的一些零点。在1982年11月苏联数学家马帝叶雪维奇在苏联杂志《Kibernetika》宣布,他利用电脑检验一个与黎曼猜想有关的数学问题,可以证明该问题是正确的,从而反过来可以支持黎曼的猜想很可能是正确的。
|
 涓浗绉戝闄㈢鏅簯骞冲彴
涓浗绉戝闄㈢鏅簯骞冲彴
 涓浗绉戝闄㈢鏅簯骞冲彴
涓浗绉戝闄㈢鏅簯骞冲彴
