作者:栾春阳(清华大学物理系)
监制:中国科普博览
在上篇文章中我们介绍了超导量子计算,这是一种基于超导现象和集成电路工艺的运算方案,作为现今主流的量子计算方案之一,不仅可以与现今的集成电路工艺相兼容,从而制备出大量的量子比特,还具有良好的可操纵性和灵活性,能够进一步应用于不同场景下的科学研究。

谷歌公司的超导量子计算机。
(图片来源:参考文献[1])
虽然超导量子计算具有超强的功能,但由于在实际运算过程中始终存在外界的干扰,超导量子计算机会不可避免地出现运算错误。并且,随着运算复杂度的不断增加,量子计算机会在运算过程中积累大量的错误,从而导致运算结果与理论值产生明显的偏离。
因此,要想实现未来真正实用化的通用量子计算机,就要在运算过程中监测错误的产生,并且通过及时的反馈来降低量子计算的错误率。这种在量子运算过程中,通过人为的方式来降低运算错误,从而实现不断纠错,这个过程就叫“量子纠错”。
强如量子计算机,为什么也会“犯错”?
在上一篇文章中,我们已经知道了量子比特的基本概念。量子比特可以同时处于0态和1态的叠加态,是量子计算机的基本运算单元。在这里,为了让大家明白量子计算机为何会犯错,就不得不引入一个球体来形象化地表示量子比特的状态,这就是“Bloch球”。
与我们所处的地球类似,Bloch球也有南北极和赤道,并且球面上的每一个点都唯一地表示量子比特的某一状态。一般而言,Bloch球的南极和北极点分别表示量子比特所处的1态和0态,而Bloch球中间“赤道”上的点则表示有50%的概率处于1态,同时也有50%的概率处于0态。
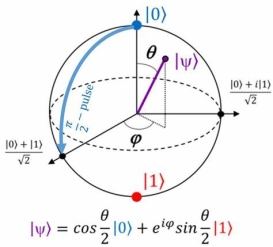
Bloch球: 用以描述单量子比特状态的
(图片来源:参考文献2)
而为了能够区别球面上不同的点,我们参考地球仪的纬度和经度的概念,引入了两个角度:![]() 和
和 ![]() 。如此一来,我们就可以用纬度
。如此一来,我们就可以用纬度![]() 和经度
和经度 ![]() 来精确地描述量子比特的特定状态。
来精确地描述量子比特的特定状态。
相信细心的小伙伴已经发现,对于Bloch球“赤道”上的所有点,虽然都表示0态和1态的叠加(纬度![]() 始终为90度),但由于外界环境的干扰,导致经度
始终为90度),但由于外界环境的干扰,导致经度 ![]() 开始出现偏移。这样的话,虽然量子比特看起来还是处于0态和1态的叠加,实际上已经偏离最初的状态,从而导致量子计算机在运算过程中出现难以预想的错误。这种由于经度
开始出现偏移。这样的话,虽然量子比特看起来还是处于0态和1态的叠加,实际上已经偏离最初的状态,从而导致量子计算机在运算过程中出现难以预想的错误。这种由于经度 ![]() 偏移导致量子计算特有的错误,有一个专门的名称——相位错误。
偏移导致量子计算特有的错误,有一个专门的名称——相位错误。
除此之外,量子计算机在实际的运算过程中,还必须经过一系列复杂的量子逻辑门的处理,这就需要极高的操纵精度,以保证算法的顺利运行。然而,即使是近乎完美的人为操纵,也无法保证100%的准确性,因此每一步的操纵都会积累微小的误差。随着操纵时间的不断增加,大量的操纵误差就会积累在运算过程中,从而导致量子计算机的最终输出结果出现明显的偏离。

(图片来源:Veer图库)
超导量子比特极易受到外界噪声干扰,而出现上述的一系列错误。因此,我们需要寻找合适的量子纠错方案,来有效保护量子计算机不受到外界噪声的干扰。
经典计算机的纠错方案——质量不够,数量来凑
“她叫马冬梅,马冬梅,马冬梅!”相信肯定有不少的小伙伴,在通讯信号不佳的时候,会将关键的数字信息重复多次,以保证对方可以准确收到我们正确的信息。

(图片来源:Veer图库)
这是因为,即使对方无法收到我们完整的通讯信息,甚至可能出现听错的情况,也仍然有极大的可能性获取正确的数字序列。这种将关键数字进行重复编码的方式,虽然信息有点冗余,却能够降低信息传递中的错误率,这就是重复编码的纠错方案。
而在经典计算机中,这种纠错方案也十分常见。这是因为,经典计算机采用二进制的运算方式,其基本的运算单元是只能表示1态或者0态的比特(bit)。然而,由于外界环境的干扰,经典计算机可能会出现1态和0态互相颠倒的情况,从而出现不可避免的运算错误。
而当我们采用重复编码的纠错方案时,这种运算的错误率就会大大降低。打个比方,我们可以用0态重复编码成“000”,并且用“111”来表示1态,这样一来,我们就可以根据少数服从多数的原则,来确定编码信息的读取。例如,原本表示0态的“000”编码,由于发生错误而变成“010”,但是编码中“0”的数目仍然大于“1”,因此根据少数服从多数的原则,这个编码仍然可以正确地表示0态。

(图片来源:Veer图库)
当然,如果外界环境的干扰十分强烈,以至于这种重复编码的纠错方案仍然不能降低运算的错误率,这就需要更加复杂的编码方式。因此,对于经典计算机而言,纠错方案已经成为必不可少的运算过程之一,从而保证运算结果的正确性。
辅助比特、逻辑比特:双剑合璧,量子纠错!
量子计算机的纠错过程和经典计算机的情况并不完全一致。对于量子计算机而言,纠错的过程并不是想象的这么简单。更加糟糕的是,在大多数的情况下,对正在运算中的量子计算机进行纠错,往往会适得其反。
这是因为,量子计算机的基本运算单元是量子比特,量子比特在参与运算的过程中,处于1态和0态的叠加态,一旦量子比特的状态被探测到时,这种奇妙的叠加性就会丢失,从而只能确定性地处于1态或者0态。
因此,正在运算中的量子比特不能被实时地探测,而不经过探测就无法确切地知道运行中发生的错误,从而无法进行正确的纠错。这就陷入一个死循环的怪圈中,如果对运算中的量子计算机进行盲目的纠错,很有可能出现越纠越错的尴尬情况。

(图片来源:Veer图库)
为了解决这个令人头疼的问题,科学家们想出来一个绝妙的方法。
将若干个量子比特编成一组,从而构成纠错运算中一个的基本单元,被称为“逻辑比特”。在纠错过程中,我们避免对基本单元中参与运算的量子比特进行直接测量,而是对其余起到辅助作用的量子比特进行测量,从而间接地读取运算中的错误,这些起到辅助作用的量子比特被称为“辅助比特”。
也就是说,一组功能不同的量子比特构成“逻辑比特”,并且参与到纠错运算中,而这些量子比特根据功能不同可以分为:真正参与运算的量子比特和起到探测错误作用的“辅助比特”。量子计算机自身的量子比特数目并不能反映出真实的计算能力,需要综合考虑运算的错误率和纠错成本,将量子比特数目转化成为“逻辑比特”数目才可以。

超导量子比特的电路设计
(图片来源:参考文献[2])
因此,量子计算机要想实现真正的量子纠错,就需要远超过理想状态下的量子比特数目,这也间接提高了实现真正实用化的量子计算机的技术难度。举个例子,最早的量子纠错编码方案就采用9个量子比特来构造出1个“逻辑比特”,而这种最早的编码方案也表现出了良好的纠错能力,也被称为Shor纠错编码。
然而,现今的量子计算机仍然无法消除外界环境的干扰,并且自身的量子比特数目还不够高,因此,我们距离实现能够真正实用化的量子计算机还有很长的一段路要走。也就是说,量子计算机现在仍然处于研究的起步阶段,这种发展状态也被称为“含噪声的中等规模量子计算( NISQ )”。
幸运的是,随着实验技术的不断进步,量子计算机的纠错方案也从最初的Shor方案不断升级成为更有效的纠错编码。对于超导量子计算而言,现今主流的量子纠错方案是二维表面的纠错编码(surface code),而就在近期,科学家们已经在量子纠错领域取得了里程碑式的成果。
量子纠错,越纠越错?NO!
近期,来自谷歌量子人工智能的研究团队采用超导量子计算方案来实现量子纠错,他们在同一个超导量子系统上对比了3个和5个“逻辑比特”在纠错方案下的综合运算错误率。研究结果显示,在3个“逻辑比特”的纠错运算中,平均的运算错误率为3.028%。而在5个“逻辑比特”的纠错运算中,其错误率降低至2.914%。
也就是说,随着纠错运算规模的不断扩大,量子计算机开始出现越纠越对的情况,从而验证了量子纠错方案的可行性。尽管纠错运算的错误率仍然很高,但是这意味着,现在的量子计算机已经不再进行盲目的纠错运算,而是已经突破了量子纠错的“平衡点”。

(图片来源:Google Quantum AI)
当然,这个实验也仍然有很多需要提升的地方。首先,该团队采用17个量子比特才编码实现了3个“逻辑比特”,而为了实现5个“逻辑比特”,甚至需要高达49个量子比特参与编码,这极大提高了所需量子比特的数目。其次,该团队现今只实现了对量子比特的纠错过程进行追踪,并没有进行后续真正实用化的算法运算。
除此之外,随着“逻辑比特”的数目从3增加到5,量子计算机的运算错误率只出现了微小的降低,这还远远达不到真正实用化的量子计算机的要求。
科学家预计,要想实现未来具有商业价值的量子计算机,大约需要1000个“逻辑比特”参与实际的纠错运算,也就意味着,量子计算机需要拥有100万个量子比特,并且要保证每次运算的错误率降低至0.001%才可以。
结语
这项研究成果,标志着人类已经跨过了量子纠错的门槛,进入到“含噪声的中等规模量子计算( NISQ )”的发展阶段。随着技术的不断提升,我们有理由相信,量子计算机的容错运算能力将不断增强,从而最终拥有大约1000个“逻辑比特”的超强算力。
同时,基于超导量子方案的量子计算机也进一步展现了自身潜在的商业价值。这也让人们开始期待,“量子时代”将会以何种方式悄然而至?我们下篇文章再来解析。
参考文献:
[1]R. Courtland, "Google aims for quantum computing supremacy [News]," in IEEE Spectrum, vol. 54, no. 6, pp. 9-10, June 2017.
[2]Beckers, Arnout & Tajalli, Armin & Sallese, Jean-Michel. (2019). A Review on Quantum Computing: Qubits, Cryogenic Electronics and Cryogenic MOSFET Physics.
[3]Gambetta, J.M., Chow, J.M. & Steffen, M. Building logical qubits in a superconducting quantum computing system. npj Quantum Inf 3, 2 (2017).
[4] Google Quantum AI. Suppressing quantum errors by scaling a surface code logical qubit. Nature 614, 676–681 (2023).


